Yeah, finally! About 2 weeks after my set due date, it's finally here. I'm proud.
Here's link for the blog, and enjoy the spresent =], make it full screen for better effectiveness.
my dev blog link
my spresent link
Sunday, June 10, 2007
Manny published calculus dev
Saturday, June 9, 2007
Christian's DEV Project
Please visit my DEV Project at christiansdev.blogspot.com. Thanks!
Monday, June 4, 2007
Wednesday, May 30, 2007
albert M's D.E.V. Project
Labels: albert M., DEV Project, Precal40s
Monday, May 28, 2007
Sunday, May 27, 2007
Katrin's DEV Project
DEV working properly now =) Thanks Mr.K!
CLICK THIS LINK TO VIEW FULL SCREEN:
https://www.spresent.com/view/?p=/katchona18@hotmail.com/DevelopingExpertVoices
Labels: APCALC, Calculus, density function, DEV, DEV Project, Integration, katrin, volumes of revolution
Tuesday, May 22, 2007
Donna's DEV
yaayyy it's so late and im finally done! =D
click to go to the website CLICK!
Labels: am40sw07, DEV Project, Donna, Matricies, Periodic Functions, Personal Finance, Vectors
Jann's DEV Project vCalculus
Heya everyone! Here's my 2nd DEV project! I hope everything is alright! =D
http://jannapdev.blogspot.com/2007/05/janns-dev-project-v0calculus.html
Labels: APCALC, DEV Project, jann
Monday, May 21, 2007
chris a.'s d.e.v
Hey guys this is my D.E.V. just click here ----->http://www.freewebs.com/johna40sapplied/
Labels: am40sw07, CHRIS A., DEV, DEV Project
Brittany's D.E.V
Hello everyone here's my Developing Expert voices project, wow a lot of work. But my pictures don't want to show the website is not cooperating with me, so the completed one will be posted as soon as possible. Sorry:(
Labels: am40sw07, Britt, DEV Project
liiinger's DEV Project
I'm done, I'm done, I'm done!!!!!!!!! Well, what are you waiting for? Click on the link ;)
http://liiinger.blogspot.com/
Sunday, May 20, 2007
JEEENG'S D.E.V PROJECT
Yay! I'm done my project finally!
Click ==> HERE
Labels: Conics, counting, JEEENG, pc40sw07, Probability, Trigonometry
Saturday, May 19, 2007
Nadiya's DEV Project
OK, I am finished my DEV finally. Please excuse any Grammer or Spelling errors. The spell check on freewebs doesn't like my computer and so i couldn't fix that. So I will fix that on Tuesday, sometime.
Enjoy
--> CLICK HERE <-- to get to my DEV PROJECT
Labels: am40sw07, DEV, DEV Project, nadiya
Friday, May 18, 2007
jOweLL's DEV Project
yEs!.. finally im done........ :D
I had a hard time thinking of how to come up with those problems and to solve them as well. Hope you find them challenging enough as I did..... :p
Labels: am40sw07, DEV Project, jOweLL
Wednesday, May 16, 2007
Tuesday, May 15, 2007
Jennifer's DEV Project
Yay, I'm done. Sorry it's like a minute late
Labels: am40sw07, DEV, Jennifer, Matrices, Probability, Statistics
Monday, May 14, 2007
Friday, May 11, 2007
DEVELOPING EXPERT VOICES!!! (Finally)
Oh My Goodness!!! I finally, finally, finally finished my project!
Well, here it is, over 60 hours of headaches and hand-cramps:
FRANCIS' BIRTHDAY
Enjoy! :D
Thursday, May 10, 2007
Developing Expert Voices
BubbleShare is ballin.
Why did you choose the concepts you did to create your problem set?
The concepts I've chosen were all from units I had the easiest time learning and understanding. Everything on this project is where I think my main knowledge in this class stands.
How do these problems provide an overview of your best mathematical understanding of what you have learned so far?
By using the terms and concepts for the units I used, I put myself to the test to create questions I know I can do but is also a challenge at the same time. It shows that I do have strong points in some units and that there are also weaker points.
Did you learn anything from this assignment? Was it educationally valuable to you?
I learned that time is a huge value for this assignment considering the mass amount of time and effort is needed. I think it is educationally valuable to me because I can see where my classmates are as well and learn off what they know most in this class.
Labels: DEV Project, Logaritims, pc40sw07, Trigonometric Identities
Monday, May 7, 2007
Al Andrei's DEV Project
Click Here to view my DEV project.
Labels: Al Andrei, am40sw07, DEV Project, Matrices, Probability, Statistics, Vectors
Tim-Math-Y's DEV
Glad I'm done! Enjoy!
http://timcdevproject.blogspot.com/
Friday, May 4, 2007
John D.'s DEV
YES! I'm so glad I'm finally done the project! I can now hand in my job application! Haha! This was a fun project though.
http://www.freewebs.com/johndevproject
Tuesday, May 1, 2007
M@rk's DEV
Why did you choose the concepts you did to create your problem set?
I choose these concepts to create my problem set because I feel that I have a better grasps of these concept than any other ones we had. I feel like I'm more confident on teaching someone a concept that i really understand.
How do these problems provide an overview of your best mathematical understanding of what you have learned so far?
I think that this project is a good measuring stick of the mathematical understanding of what i learned so far.It made me think that I still have a long way to go to become an expert but i will my best to attain that level.
Did you learn anything from this assignment? Was it educationally valuable to you? (Be honest with this. If you got nothing out of this assignment then say that, but be specific about what you didn't like and offer a suggestion to improve it in the future.)
This project was definitely a good experience. It was kinda like a review for the exam because you look back at the concepts that you don't get before and try to teach it to other people.What I didn't like about this project is that we are the first class to do this project. At first I really had no idea on how to start my project but when I saw Graeme's project ideas just kept clicking on my head. Overall, this was an excellent project because it pushes you to work even harder and explore the different applications of the concepts that you've learned so far.
MR. K,
I'm just going to edit this tommorow and post it with my podcasts.
Monday, April 30, 2007
Developing Expert Voices
OK! It's done. Everything appears to be working this time, so here goes.
http://www.slideshare.net/suzanne/developing-expert-voices-45702/
Sunday, April 29, 2007
VINCENT's Developing Expert Voices Project
THIS PROJECT HAS BEEN UPDATED. I'm just so glad this is off my shoulders now! I hope I met the requirements that the EXPERT category wants out of me...
VINCENT'S D.E.V. BLOG!
DEV---Aichelle.
Hello everyone! My due date for this DEV is tomorrow [30th] but I thought that I'd just post this now so I don't forget.
Here is the link to my DEV:
http://www.freewebs.com/aichellepc40sw07/index.htm
Hope it's good enough for you. Enjoy, thanks.
Robert's Developing Expert Voices Project
Hello everyone! Today is my due date so I'm posting my project. Now there are some weird symbols on my project but you can just ignore them and follow step by step and you will be fine. Also, the slide show does not fit on the blog so just open it up by clicking on slideshare and you will be able to see the whole show clearly. Hope you enjoy the project!
Labels: DEV Project, pc40sw07, Robert, Trigonometric Identities
Thursday, April 26, 2007
Developing Expert Voices
SAMUS' BLOG
Labels: counting, DEV Project, Identities, Logaritims, pc40sw07, SAMUS, Transformations
Tuesday, April 24, 2007
Jann's DEV Project
Hello everyone! I've finally finished my project. I hope it has no mistakes. XD
Question 1: The "Super" Worried Father
A worried father keeps walking around in circles, waiting for his son to call home. Because he was so worried he can do 38.2 revolutions every 2 minutes from the point where the phone is (humanly impossible). Assume he walks in a constant rate. His farthest distance from the phone is 3.4 meters. Determine circular distance when he was 2.4 meters away from the phone when it rang. Assume that he started at the phone.
Question 2: Mike's Pizza Party
Mike decided to have a party at his house. He ordered two 14" pizzas for his party. He wanted it to be divided into 17 equal slices since its his favorite number. His friends love pizza so much. There will be 20 people for his party. He doesn't know how big would these slices will be. Find the area of a slice and find out how many different ways can his guests could have a slice. After all the guests got their slice, Mike would allow seconds. (He doesn't care who gets what slice since they're all equal)
Question 3: Leo the Lion's Great Marathon
Leo decided to have a big race for his kingdom. They will be using a circular track, where the "Great Tree" is a point on the outer-most track. This will be the starting point. Leo was worried that he might lose to the other contestants. He consulted his friend Shane the Snake, his trustworthy adviser. Shane estimated that the lanes are 1.2 meters away from each other. There will be 3 contestants in the 4-lane track. The diameter of the whole track is 125 meters.
Few days before the race, Leo and Shane went to the track and did some test runs. They realized that the lanes have different obstacles on the way. Shane said that Leo can do:
2.6 revolutions every 5 minutes on the 1st lane
1.7 revolutions every 3 minutes on the 2nd lane
3.8 revolutions every 2 minutes on the 3rd lane
2.3 revolutions every 5 minutes on the 4th lane
Which lane will make sure that Leo will do his best run? How many different ways would the other contestants pick their lanes, assuming they don't know that the lanes have obstacles? What would be the formula for Leo's choice of lane?
Sol.
This is a diagram of the situation...

 Now that we know the number of ways, we could find a formula for Leo's choice of lane, lane 3.
Now that we know the number of ways, we could find a formula for Leo's choice of lane, lane 3.
 Question 4: Chemical X Problem
Question 4: Chemical X Problem
Chemical X contains a certain bacteria that allows it to grow exponentially. The chemists recorded that the chemical was 10.58mL after an hour. Since these chemists are lazy, they stopped gathering information after this first hour. If they had 10mL to start with, predict the how long it would take for the chemical to be 17mL.
I really gave a lot of time to do this project. For me, it's pretty hard to think of a question. I thought it would be a piece of cake. The hard part is, I don't know if this is really an "expert" level project in other's point of view. At least I followed the rubric with the best of my abilities.
I hope everything is A-OK. Great day everyone! =D
Labels: DEV Project, jann
dev
hey sorry about that people for being so late,Had alot of problems posting it up from powerpoint. thank you MR.K for the source.
TENNY'S DEV Project
HERE it is
Labels: am40sw07, DEV Project, Matrices, Probability, Statistics, Tennyson
MrSiwWy's DEV
Yay! I'm finally finished my DEV! I hope everything is okay and there's no mistakes or anything =/ I worked more than extremely hard on this... )= sleep deprived to the max. Well I hope my DEV is at least up to par, if not I wasted a looot of time =/ Well here is the link to my DEV blog... enjoy! I guess...
Monday, April 23, 2007
Sandy's DEV Project
So here it is. It's not exactly positioned the way it should be, but Slideshare kept doing that to me. So this is it, it's finished. This should due for now until I find something better to use. (:
MY REFLECTION:
I know this is actually kind of late but I forgot all about it since I've been caught up in other things. Well honestly, this project hasn't really benefited me in any way. I did my questions like any other questions that we did on tests, pretests, quizzes and in the exercises. In other words, they were Journey person questions. So it didn't really teach me anything I didn't know. If I was taking this course next year maybe then I would've tried to go for the Expert level questions. But I wasn't about to push myself this semester to do something like that. The only reason is because I had other projects to do that I put above this project. Don't get me wrong, it was a fun project. We were able to use our creativity and computer skills to make math questions into something more interesting and at the same time, teach people. I think I could have done better on this project if it was the only thing I had to worry about. I also find it hard to keep slides to a minimum amount of text. It's hard when you're trying to teach someone over the computer and at the same time keep the text small so they won't get bored and leave. In person, it's a lot easier. Another this is, I think I would've enjoyed this project being done by hand. I like those kind of projects more than computer ones. Just a little idea for maybe later on. I think we can express more creativity with things on paper rather than on the computer. Not everyone is as good at computers as others. So maybe there should have been a choice given? Honestly, I think I would've had more fun cutting and pasting things onto paper for this project, but that's me. Anyway... overall I think the project was a pretty good idea, it just kind of came at a bad time, but it's good!
Labels: DEV Project, Identities, Logaritims, pc40sw07, sandy, Transformations
Sunday, April 22, 2007
Dino's DEV Project
Hello it is Monday April 23rd and today is may due date for my DEV Project. I will not keep you waiting, so here it is, I hope you like it:
This is my project from slideshare, it is in slide form, if you want the full screen version here it is.
If you would like to listen to the questions as you are reading them or working on the problems, here is the link.
Here is the same project, only in movie form.
To see the actual video, because this video may be hard for some people to see here it is at blip.tv.
I hope you had enjoyed my DEV project!
Labels: DEV Project, Dino, Logaritims, Transformations, Trigonometry
Thursday, April 19, 2007
DEV Post: April 19, 2007
I'm done!! Thank you God! HAHA, so here's my DEV Project, enjoy :) Click Here. - Grace
Labels: am40sw07, DEV Project, Grace, Matrices, Probability, Statistics
Monday, April 9, 2007
Developing Expert Voices; Ivy's Project
HELLO!!! People it's April 9, 2007 and it's my due date for my D.E.V.
So Click Here**** to go to my project hopefully it's good enough.
Labels: DEV Project, Ivy
Thursday, March 29, 2007
Grey-M's DEV Project
Hello everyone and welcome to my Developing Expert Voices project! Why don't you give the questions below a try, I dare ya. If you can't get them then take a look at the answers that I have come up with because I believe that they are right. The sound adds a little bit to the questions at times but it is kind of eradic volume-wise (and I really don't sound too thrilled in them).
Question 1 – The Velodrome
Two bicyclists are going around the track in a bike race. One bicyclist decides to pull away when he starts going down the slope at one end of the track improving his lap time to twenty seconds. Their speeds (m/s) are represented by the following sinusoidal functions where x is twentieths of the track and y is the speed in m/s:
Racer 1: f(x) = 10sin((pi/5)(x))+40
Racer 2: g(x) = 5sin((pi/5)(x))+35
How many laps will it take for racer 1’s speed to get to double racer 2's speed if racer 1 is picking up speed at a rate of x for every x twentieths of the track when he started to pull away and the range of racer 2’s speed is now half that it was before?See the larger version of the slideshow here
Question 2
Solve for x, y and z:
eiπ(4(cos2(y-(pi/2)) + cos2(y))) – z = 4x(cos2((pi/5)(y –2.5) + cos2((pi/5)(y))y ^ y
3(sin2(y)+cos2(y))y! + x = 2z(csc2(y) - cot2(y))xyzSolution:
You may look at this and say to yourself "To solve for three variables you need three equations" if you remember back to systems. But if you look carefully this is an easy problem and a solvable one.
eiπ(4(cos2(y-(pi/2)) + cos2(y))) – z = 4x(cos2((pi/5)(y –2.5) + cos2((pi/5)(y))y ^ y
First, simplify what is in the brackets in the first term. The first term within the brackets is a shifted squared cosine function. Well with the shift it has it is a squared sine function.
eiπ(4(sin2(y) + cos2(y))) – z = 4x(cos2((pi/5)(y –2.5) + cos2((pi/5)(y))y ^ y)
Now sin2(y) + cos2(y) you should recognize as the rudimentary trig identity, so it is equal to 1 and 4 times 1 is 4.
eiπ(4) – z = 4x(cos2((pi/5)(y –2.5) + cos2((pi/5)(y))y ^ y
The last thing you have to do to this is recognize Euler's identity(eiπ+1 = 0).
-4 – z = 4x(cos2((pi/5)(y –2.5) + cos2((pi/5)(y))y ^ y
That side is really easy now so we'll go to the other side to the first term within the brackets. It is a squared cosine function that has a parameter B of (pi/5) which means that the period of the function is going to be 10 ( 2pi/B --> 5*2pi/pi --> 10). It has a phase shift of 2.5 to the right. Hmmm... well that's just perfect. That makes is a squared sine function with the same parameter B and no phase shift. Once again this is the rudimentary trig identity so it is equal to 1.
-4 – z = 4x(1)y ^ y
Now 1 to any exponent is still 1.
-4 – z = 4x * 1
Anything times 1...
-4 – z = 4x
So the first equation is now easy as pi (couldn't resist, I'm so corny...). What we do to the next equation is the same thing...
3(sin2(y)+cos2(y))y! + x = 2z(csc2(y) - cot2(y))xyz
Identify the trig identities.
3(1)y! + x = 2z(1)xyz
One to any exponent is 1 (y! is a factorial).
3(1) + x = 2z(1)
Anything times 1 is itself.
3 + x = 2z
Now you have two easy equations. Y has been completely eliminated meaning that the value of y is an element of all numbers real or imaginary (Since it doesn't effect the equations at all it can be anything).
Then just solve the system. (The quality of the picture really is downgraded for some reason, if you want to look at the good quality image go here)

So your answer would be -11/9 = x, 8/9 = z and y is an element of the real or imaginary numbers.
Question 3
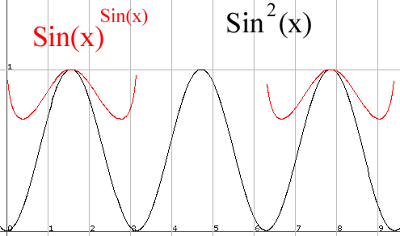
Solve for x: sin(x)sin(x) = sin2(x)
Solution
One way you could solve this is to let sin(x) = a. Then you have a^a = a^2. The only values that will work for this are 1 and 2 (2^2 = 2^2, 1^1 = 1^2) because any other numbers and they are inequalities (0.001^0.001 <> pi^2). If you ask "Why not 0?" Then my answer is I don't know because not even the experts are certain, or atleast agree, what the value of 0 to the 0 is, so I cannot say that 0^0 = 0^2. Then we reject the answer of 2 because sin(x) will never give us an answer greater than 1. So within one period of the sine function sin(x)sin(x) the only possible value for sin(x) will be 1. The value in which sin(x) = 1 is pi/2. Since this is a sine function this will repeat. But how often? It will not repeat every period because when the sine function enters the negative outputs we'll begin to get imaginary answers because you cannot have negatives under the radical sign (the only one that will still work would be -1, any others are decimals and when changed from exponential to radical form they will have the negative base under the radical). Since both are sinusoidal functions this will repeat every 2kpi where k is an element of integers because we eliminated it repeating every period or kpi where k is an element of the integers.
So our answer formally is x = (pi/2) + 2kpi; kEI.
Graphically to support my answer...
Question 4
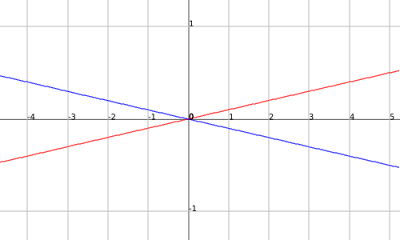
How many equations are there that at infinite points touches/intersects the functions:
f(x)= x/10 and g(x) = -x/10.
Name atleast 3 of them and you cannot use tangent.
First visualize what your trying to do.
f(x)= x/10 g(x) = -x/10
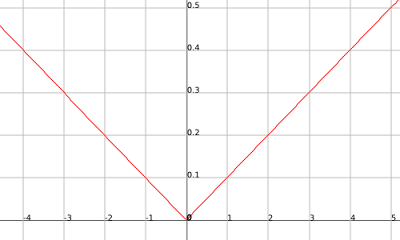
If you look you may see that these graphs are the same except for the fact that the outputs of the second graph are negative that of the first. So if you had a function that had infinite amount of points equal to that of the first graph in the positive inputs then when it crosses the y-axis and starts getting negative inputs makes those outputs opposite sign then you would have an infinite amount of points on both graphs. It just so happens that h(x)= |x/10| does just that.
.png)
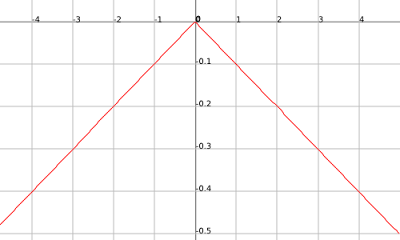
If that works then the negative of that will work also just the positive inputs will go along our second function while our negative inputs will go along our first function, j(x)= -|x/10|.
.png)
Now the answer that is the point of this question. We know that sine, cosine and tangent graphs will get positive and negative values periodically.
k(x) = sin(x) f(x)= x/10 g(x) = -x/10
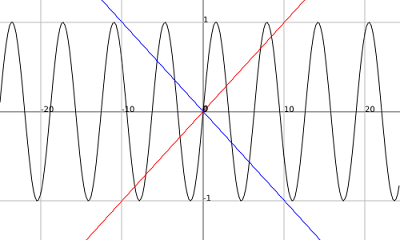.png)
This graph, k(x) = sin(x), doesn't touch these lines at infinite points. But we do know some things about this graph. For one we know that the maximum and minimum values are 1 and -1 respectively. Those are easy numbers to work with. But they occur in relation to pi which is not as easy. So since we can manipulate the sine function to suit our needs we can set the period to be an easy number like 2. Our sine function will then be m(x) = sin(pi(x)) because...
period = 2pi/B
2 = 2pi/B
B = pi
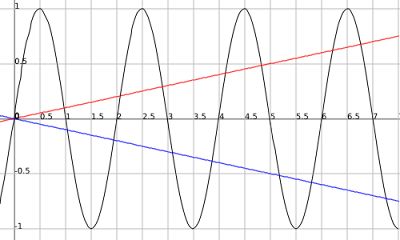.png)
Now we have our outputs of 1 and -1 alternately at every input of a+0.5 ;aEI. Now how do you change 1 to a number of your choice? You multiply by that number. So if the outputs of m(x) = sin((pi)(x)) are 1 then you just multiply whatever sin((pi)(x) )gives you by (x/10) and when sin((pi)(x)) gives an output of 1 it will be the same as the output of f(x) = (x/10). The new function you would now get is n(x) = m(x)f(x) or n(x) = (x/10)(sin((pi)(x)). Now since the bottom line is the same equation just with negative outputs of f(x) = x/10, or in other words f(-x) = g(x), when (sin((pi)(x)) equals -1 then n(x) will equal f(-x) or g(x) ((-x)/10 = -x/10). So n(x) = (x/10)(sin((pi)(x)) will touch both lines infinitely because (sin((pi)(x)) will infinitely give outputs of 1 and -1.
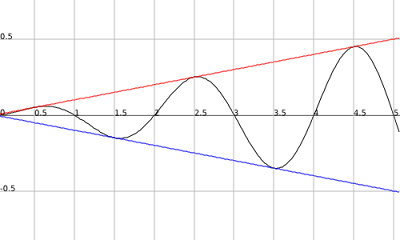.png)
Now n(x) = (x/10)(sin((pi)(x)) can be made simpler and in making it simpler we also find that there is an infinite amount of functions that will infinitely intersect the functions f(x) and g(x). We said that when (sin((pi)(x)) in our function n(x) = 1 or -1 that we'll get the outputs of f(x) and g(x) at those points respectively. Well does parameter B in a sine function affect the maximum and minimum values of 1 and -1 in a regular sine function? No. So our function could be q(x) = (x/10)(sin(z)(x)); zER. Now there is also another way to see that there is an infinite amount of possibilities. If you had any set of lines with a steeper slope than f(x) = x/10 then for our sine function to touch that line then it would have to cross f(x) and g(x). For a line to have a steeper slope than f(x)= x/10 it would have to have x divided by a number less than 10 but larger than -10. An example: r(x) = (x/5)(sin(x))
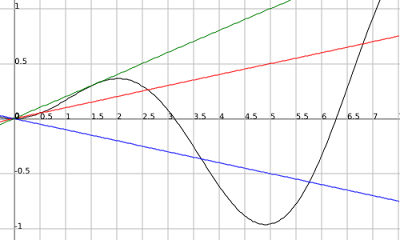.png)
So since this is true a function that will infinitely cross the functions f(x), g(x) is:
s(x) = (x/t)(sin(z)(x));-10<=t<=10; tER; zER This same answer will apply to cosine with any phase shift because phase shift makes no difference in this and cosine just like sine will infinitely get outputs of 1 and -1. u(x) = (x/t)(cos(z)(x));-10<=t<=10; tER; zER Summary • Why did you choose the concepts you did to create your problem set? I chose the concepts that I did because I wanted to cover a lot of what we've done in grade 12 so far no matter how comfortable or uncomfortable I was with them. • How do these problems provide an overview of your best mathematical understanding of what you have learned so far? Well I found them rather hard so I guess that it would show the upper level of my skill which would be what I have learned so far. • Did you learn anything from this assignment? Was it educationally valuable to you? I learned lots from this. For one I learned that making problems that are hard but not impossible for yourself is *really* hard. Second I learned that when making these you should really work backwards from the answer because solving a problem that is on the brink of what you can do with no clue as to what the answer is will make you end up at the wrong answer a high percentage of the time. That first question was actually a five part question with the one I used being the last one. But I made the questions and then tried to get the answers. So I found out one was wrong and it made all the others wrong except for the last question (two days of spring break wasted). Then in my first answer I created for question 3 I found that I completely screwed that up. Overall I think that this was valuable because I don't know a time when I have thought so hard (and I truly hope I didn't get any of those wrong). One thing I must say though is that being able to do the problems is one thing but explaining them is another. When I did the problems I knew exactly what I was doing but when explaining them the words escaped me. I almost think that it would have been worth doing journeyman level questions for the boost in the mark of annotation because I don't know if my answers are going to get through to everyone. I know what I mean but others may not. With an easier question that you have a stronger foundation in you'll be able to explain it much better. Give me feedback. If you don't get how I solved the questions or if you think I got them wrong then tell me in the comments. Maybe I'll be able to explain them in the comments and Mr.K will allow another modifier in the annotation/solution mark for ongoing annotation/solutions.
Labels: DEV Project, Exponents, Grey-M, Identities, Logic, Systems, Transformations, Trigonometry
Tuesday, March 27, 2007
The Assessment Rubric
Here is the updated version 1.1 of our rubric ...
Teaching mathematical concepts is the main focus of this project; so we can teach other people and learn at the same time.
Achievement Descriptors
Instead of levels 1-4 (lowest to highest) we use these descriptors. They better describe what this project is all about.
Novice: A person who is new to the circumstances, work, etc., in which he or she is placed; a beginner.
Apprentice: One who works for an expert for instruction or to learn a skill or trade.
Journeyperson: Any experienced, competent but routine worker or performer.
Expert: One who possesses special skill or knowledge; trained by practice; skillful and skilled.
| Achievement | Mathematical Challenge (25%) | Annotation (40%) | Solutions (15%) | Presentation (20%) |
| Novice | Problems illustrate only an introductory knowledge of the subject. They may be unsolvable or the solutions to the problems are obvious and/or easy to find. They do not demonstrate mastery of the subject matter. | Explanation does not "flow," may not be in sequential order and does not adequately explain the problem(s). May also have improper mathematical notation. | One or more solutions contain several errors with insufficient detail to understand what's going on. | Presentation may or may not include visual or other digital enhancements. Overall, a rather uninspired presentation. Doesn't really stand out. It is clear that the student has invested little effort into planning their presentation. |
| Apprentice | Problems are routine, requiring only modest effort or knowledge. The scope of the problems does not demonstrate the breadth of knowledge the student should have acquired at this stage of their learning. | Explanation may "flow" well but only vaguely explains one or more problems. Some parts of one or more solutions are difficult to follow. May include improper use of mathematical notation. | One or more solutions have a few errors but are understandable. | The presentation style is attractive but doesn't enhance the content; more flashy than functional. It is clear that the student has invested some effort into planning their presentation. |
| Journeyperson | Problems showcase the writer's skill in solving routine mathematical problems. They span an appropriate breadth of material. One or more problems may require careful thought such as consideration of a special case or combine concepts from more than one unit but not necessarily. | Explanation "flows" well and explains the problems step by step. Solution is broken down well and explained in a way that makes it easy to follow. May have minor use of improper mathematical notation. May point out other ways of solving one or more problems as well. | All solutions are correct and easy to understand. Very few or no minor errors. | The presentation may use multiple media tools. The presentation style is attractive and maintains interest. Some of the underlying message may be lost by some aspects that are more flashy than functional. It is clear that the student has given some forethought and planning to their presentation. |
| Expert | Problems span more than one unit worth of material. All problems are non-routine. Every problem includes content from at least two different units. Problems created demonstrate mastery of the subject matter. Showcases the writer's skill in solving challenging mathematical problems. | Explanation "flows" well, explains the problems thoroughly and points out other ways of solving at least two of them. | All solutions correct, understandable and highly detailed. No errors. | The presentation displays use of multiple media tools. The presentation style grabs the viewer's or reader's attention and compliments the content in a way that aids understanding and maintains interest. An "eye opening" display from which it is evident the student invested significant effort. |
Creativity (up to 5% bonus)
The maximum possible mark for this assignment is 105%. You can earn up to 5% bonus marks for being creative in the way you approach this assignment. This is not a rigidly defined category and is open to interpretation. You can earn this bonus if your work can be described in one or more of these ways:
- unique and creative way of sharing student's expertise, not something you'd usually think of;
- work as a whole makes unexpected connections to real world applications;
- original and expressive;
- imaginative;
- fresh and unusual;
- a truly original approach; presentation method is unique, presented in a way no one would expect, e.g. song, movie, etc.
Labels: Assessment
Monday, March 26, 2007
The Assignment
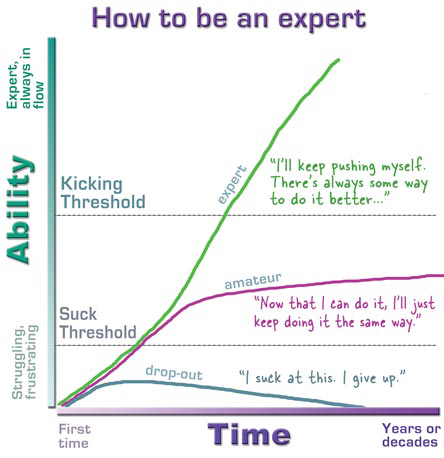
The Assignment
Think back on all the things you have learned so far this semester and create (not copy) four problems that are representative of what you have learned. Provide annotated solutions to the problems; they should be annotated well enough for an interested learner to understand and learn from you. Your problems should demonstrate the upper limit of your understanding of the concepts. (I expect more complex problems from a student with a sophisticated understanding than from a student with just a basic grasp of concepts.) You must also include a brief summary reflection (250 words max) on this process and also a comment on what you have learned so far.
Timeline
You will choose your own due date based on your personal schedule and working habits. The absolute final deadline is May 31, 2007. You shouldn't really choose this date. On the sidebar of the blog is our class Google Calendar. You will choose your deadline and we will add it to the calendar in class. Once the deadline is chosen it is final. You may make it earlier but not later.
Format
Your work must be published as an online presentation. You may do so in any format that you wish using any digital tool(s) that you wish. It may be as simple as an extended scribe post, it may be a video uploaded to YouTube or Google Video, it may be a SlideShare or BubbleShare presentation or even a podcast. The sky is the limit with this. You can find a list of free online tools you can use here (a wiki put together by Mr. Harbeck and myself specifically for this purpose). Feel free to mix and match the tools to create something original if you like.
Summary
So, when you are done your presentation should contain:
(a) 4 problems you created. Concepts included should span the content of at least one full unit. The idea is for this to be a mathematical sampler of your expertise in mathematics.
(b) Each problem must include a solution with a detailed annotation. The annotation should be written so that an interested learner can learn from you. This is where you take on the role of teacher.
(c) At the end write a brief reflection that includes comments on:
• Why did you choose the concepts you did to create your problem set?
• How do these problems provide an overview of your best mathematical understanding of what you have learned so far?
• Did you learn anything from this assignment? Was it educationally valuable to you? (Be honest with this. If you got nothing out of this assignment then say that, but be specific about what you didn't like and offer a suggestion to improve it in the future.)
Experts always look back at where they have been to improve in the future.
(d) Your presentation must be published online in any format of your choosing on the Developing Expert Voices blog. url: tba.
Experts are recognized not just for what they know but for how they demonstrate their expertise in a public forum.
Levels of Achievement
Instead of levels 1-4 (lowest to highest) we will use these descriptors. They better describe what this project is all about.
Novice: A person who is new to the circumstances, work, etc., in which he or she is placed.
Apprentice: To work for an expert to learn a skill or trade.
Journeyperson: Any experienced, competent but routine worker or performer.
Expert: Possessing special skill or knowledge; trained by practice; skillful and skilled.
Labels: Assignment

