Hello everyone and welcome to my Developing Expert Voices project! Why don't you give the questions below a try, I dare ya. If you can't get them then take a look at the answers that I have come up with because I believe that they are right. The sound adds a little bit to the questions at times but it is kind of eradic volume-wise (and I really don't sound too thrilled in them).
Question 1 – The Velodrome
Two bicyclists are going around the track in a bike race. One bicyclist decides to pull away when he starts going down the slope at one end of the track improving his lap time to twenty seconds. Their speeds (m/s) are represented by the following sinusoidal functions where x is twentieths of the track and y is the speed in m/s:
Racer 1: f(x) = 10sin((pi/5)(x))+40
Racer 2: g(x) = 5sin((pi/5)(x))+35
How many laps will it take for racer 1’s speed to get to double racer 2's speed if racer 1 is picking up speed at a rate of x for every x twentieths of the track when he started to pull away and the range of racer 2’s speed is now half that it was before?See the larger version of the slideshow here
Question 2
Solve for x, y and z:
eiπ(4(cos2(y-(pi/2)) + cos2(y))) – z = 4x(cos2((pi/5)(y –2.5) + cos2((pi/5)(y))y ^ y
3(sin2(y)+cos2(y))y! + x = 2z(csc2(y) - cot2(y))xyzSolution:
You may look at this and say to yourself "To solve for three variables you need three equations" if you remember back to systems. But if you look carefully this is an easy problem and a solvable one.
eiπ(4(cos2(y-(pi/2)) + cos2(y))) – z = 4x(cos2((pi/5)(y –2.5) + cos2((pi/5)(y))y ^ y
First, simplify what is in the brackets in the first term. The first term within the brackets is a shifted squared cosine function. Well with the shift it has it is a squared sine function.
eiπ(4(sin2(y) + cos2(y))) – z = 4x(cos2((pi/5)(y –2.5) + cos2((pi/5)(y))y ^ y)
Now sin2(y) + cos2(y) you should recognize as the rudimentary trig identity, so it is equal to 1 and 4 times 1 is 4.
eiπ(4) – z = 4x(cos2((pi/5)(y –2.5) + cos2((pi/5)(y))y ^ y
The last thing you have to do to this is recognize Euler's identity(eiπ+1 = 0).
-4 – z = 4x(cos2((pi/5)(y –2.5) + cos2((pi/5)(y))y ^ y
That side is really easy now so we'll go to the other side to the first term within the brackets. It is a squared cosine function that has a parameter B of (pi/5) which means that the period of the function is going to be 10 ( 2pi/B --> 5*2pi/pi --> 10). It has a phase shift of 2.5 to the right. Hmmm... well that's just perfect. That makes is a squared sine function with the same parameter B and no phase shift. Once again this is the rudimentary trig identity so it is equal to 1.
-4 – z = 4x(1)y ^ y
Now 1 to any exponent is still 1.
-4 – z = 4x * 1
Anything times 1...
-4 – z = 4x
So the first equation is now easy as pi (couldn't resist, I'm so corny...). What we do to the next equation is the same thing...
3(sin2(y)+cos2(y))y! + x = 2z(csc2(y) - cot2(y))xyz
Identify the trig identities.
3(1)y! + x = 2z(1)xyz
One to any exponent is 1 (y! is a factorial).
3(1) + x = 2z(1)
Anything times 1 is itself.
3 + x = 2z
Now you have two easy equations. Y has been completely eliminated meaning that the value of y is an element of all numbers real or imaginary (Since it doesn't effect the equations at all it can be anything).
Then just solve the system. (The quality of the picture really is downgraded for some reason, if you want to look at the good quality image go here)

So your answer would be -11/9 = x, 8/9 = z and y is an element of the real or imaginary numbers.
Question 3
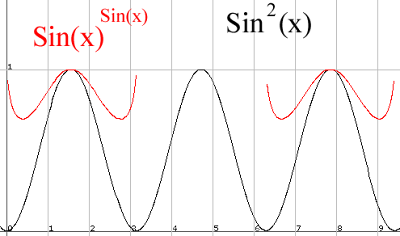
Solve for x: sin(x)sin(x) = sin2(x)
Solution
One way you could solve this is to let sin(x) = a. Then you have a^a = a^2. The only values that will work for this are 1 and 2 (2^2 = 2^2, 1^1 = 1^2) because any other numbers and they are inequalities (0.001^0.001 <> pi^2). If you ask "Why not 0?" Then my answer is I don't know because not even the experts are certain, or atleast agree, what the value of 0 to the 0 is, so I cannot say that 0^0 = 0^2. Then we reject the answer of 2 because sin(x) will never give us an answer greater than 1. So within one period of the sine function sin(x)sin(x) the only possible value for sin(x) will be 1. The value in which sin(x) = 1 is pi/2. Since this is a sine function this will repeat. But how often? It will not repeat every period because when the sine function enters the negative outputs we'll begin to get imaginary answers because you cannot have negatives under the radical sign (the only one that will still work would be -1, any others are decimals and when changed from exponential to radical form they will have the negative base under the radical). Since both are sinusoidal functions this will repeat every 2kpi where k is an element of integers because we eliminated it repeating every period or kpi where k is an element of the integers.
So our answer formally is x = (pi/2) + 2kpi; kEI.
Graphically to support my answer...
Question 4
How many equations are there that at infinite points touches/intersects the functions:
f(x)= x/10 and g(x) = -x/10.
Name atleast 3 of them and you cannot use tangent.
First visualize what your trying to do.
f(x)= x/10 g(x) = -x/10
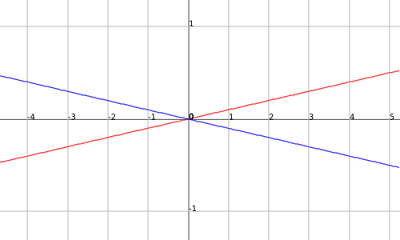
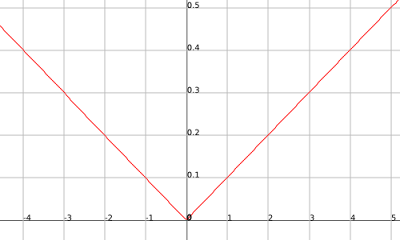
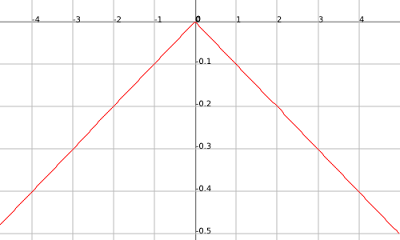
If you look you may see that these graphs are the same except for the fact that the outputs of the second graph are negative that of the first. So if you had a function that had infinite amount of points equal to that of the first graph in the positive inputs then when it crosses the y-axis and starts getting negative inputs makes those outputs opposite sign then you would have an infinite amount of points on both graphs. It just so happens that h(x)= |x/10| does just that.
.png)
If that works then the negative of that will work also just the positive inputs will go along our second function while our negative inputs will go along our first function, j(x)= -|x/10|.
.png)
Now the answer that is the point of this question. We know that sine, cosine and tangent graphs will get positive and negative values periodically.
k(x) = sin(x) f(x)= x/10 g(x) = -x/10
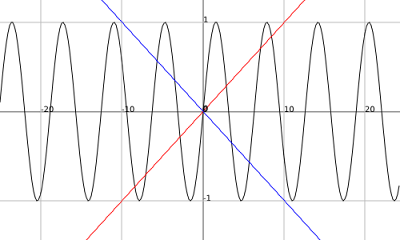.png)
This graph, k(x) = sin(x), doesn't touch these lines at infinite points. But we do know some things about this graph. For one we know that the maximum and minimum values are 1 and -1 respectively. Those are easy numbers to work with. But they occur in relation to pi which is not as easy. So since we can manipulate the sine function to suit our needs we can set the period to be an easy number like 2. Our sine function will then be m(x) = sin(pi(x)) because...
period = 2pi/B
2 = 2pi/B
B = pi
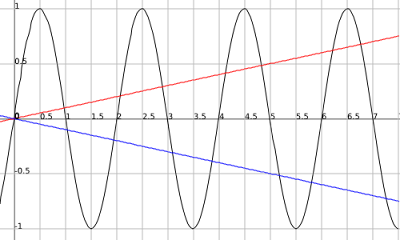.png)
Now we have our outputs of 1 and -1 alternately at every input of a+0.5 ;aEI. Now how do you change 1 to a number of your choice? You multiply by that number. So if the outputs of m(x) = sin((pi)(x)) are 1 then you just multiply whatever sin((pi)(x) )gives you by (x/10) and when sin((pi)(x)) gives an output of 1 it will be the same as the output of f(x) = (x/10). The new function you would now get is n(x) = m(x)f(x) or n(x) = (x/10)(sin((pi)(x)). Now since the bottom line is the same equation just with negative outputs of f(x) = x/10, or in other words f(-x) = g(x), when (sin((pi)(x)) equals -1 then n(x) will equal f(-x) or g(x) ((-x)/10 = -x/10). So n(x) = (x/10)(sin((pi)(x)) will touch both lines infinitely because (sin((pi)(x)) will infinitely give outputs of 1 and -1.
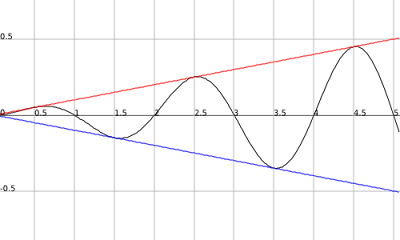.png)
Now n(x) = (x/10)(sin((pi)(x)) can be made simpler and in making it simpler we also find that there is an infinite amount of functions that will infinitely intersect the functions f(x) and g(x). We said that when (sin((pi)(x)) in our function n(x) = 1 or -1 that we'll get the outputs of f(x) and g(x) at those points respectively. Well does parameter B in a sine function affect the maximum and minimum values of 1 and -1 in a regular sine function? No. So our function could be q(x) = (x/10)(sin(z)(x)); zER. Now there is also another way to see that there is an infinite amount of possibilities. If you had any set of lines with a steeper slope than f(x) = x/10 then for our sine function to touch that line then it would have to cross f(x) and g(x). For a line to have a steeper slope than f(x)= x/10 it would have to have x divided by a number less than 10 but larger than -10. An example: r(x) = (x/5)(sin(x))
.png)
So since this is true a function that will infinitely cross the functions f(x), g(x) is:
s(x) = (x/t)(sin(z)(x));-10<=t<=10; tER; zER This same answer will apply to cosine with any phase shift because phase shift makes no difference in this and cosine just like sine will infinitely get outputs of 1 and -1. u(x) = (x/t)(cos(z)(x));-10<=t<=10; tER; zER Summary • Why did you choose the concepts you did to create your problem set? I chose the concepts that I did because I wanted to cover a lot of what we've done in grade 12 so far no matter how comfortable or uncomfortable I was with them. • How do these problems provide an overview of your best mathematical understanding of what you have learned so far? Well I found them rather hard so I guess that it would show the upper level of my skill which would be what I have learned so far. • Did you learn anything from this assignment? Was it educationally valuable to you? I learned lots from this. For one I learned that making problems that are hard but not impossible for yourself is *really* hard. Second I learned that when making these you should really work backwards from the answer because solving a problem that is on the brink of what you can do with no clue as to what the answer is will make you end up at the wrong answer a high percentage of the time. That first question was actually a five part question with the one I used being the last one. But I made the questions and then tried to get the answers. So I found out one was wrong and it made all the others wrong except for the last question (two days of spring break wasted). Then in my first answer I created for question 3 I found that I completely screwed that up. Overall I think that this was valuable because I don't know a time when I have thought so hard (and I truly hope I didn't get any of those wrong). One thing I must say though is that being able to do the problems is one thing but explaining them is another. When I did the problems I knew exactly what I was doing but when explaining them the words escaped me. I almost think that it would have been worth doing journeyman level questions for the boost in the mark of annotation because I don't know if my answers are going to get through to everyone. I know what I mean but others may not. With an easier question that you have a stronger foundation in you'll be able to explain it much better. Give me feedback. If you don't get how I solved the questions or if you think I got them wrong then tell me in the comments. Maybe I'll be able to explain them in the comments and Mr.K will allow another modifier in the annotation/solution mark for ongoing annotation/solutions.